ЕГОРОВА ВИКТОРИЯ ВАЛЕРИЕВНА

учител по математика

най-висока квалификационна категория

ТЕМА: „ИДЕНТИЧНА ТРАНСФОРМАЦИЯ

ЛОГАРИТМИЧНИ ИЗРАЖЕНИЯ"

Знания и умения, които студентите трябва да усвоят след обучението този урок:

познава дефиницията на логаритъм на число, основно логаритмично тъждество, свойства на логаритмите;

да може да извършва трансформации на изрази, съдържащи логаритми и да пресмята логаритми.

Литература:

1. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др.Алгебра и началото на анализа: учебник за 10-11 клас образователни институции. – М.: Образование, 2001.

2. Кочагин В.В., Кочагина М.В., Интензивен подготвителен курс за Единния държавен изпит. – М.: Ексмо, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Алгебричен симулатор: Наръчник за ученици и кандидати. – М.: Илекса, 2005.

4. Гусев В.А., Мордкович А.Г. Математика: Справочни материали: Книга за студенти. – М.: Образование, 2001.

План на урока:

Напредък на урока:

1) Логаритъм е гръцка дума, която се състои от 2 думи: "логос" - отношение, "аритмос" - число. Това означава, че логаритъмът е число, което измерва отношение. Публикация от 1614 г. съобщава, че Напиер е изобретил логаритмите. По-късно той съставя логаритмични таблици, които сега са ни известни като таблици на Брадис. За по-малко от един век таблиците се разпространиха по целия свят и се превърнаха в незаменим компютърен инструмент. Впоследствие те бяха, така да се каже, вградени в удобно устройство, което значително ускорява процеса на изчисление - слайд правило, което се използва до седемдесетте години на двадесети век.

Приложение 1.

2) Логаритъм положително числоbвъз основа на а, и и е по-голямо от нула и не е равно на единица,е степента, до която трябва да се повдигне дадено числоа за да получите номераb.

Това равенство, изразяващо дефиницията на логаритъм, се наричаосновно логаритмично тъждество .

В

ИЛИ 1

П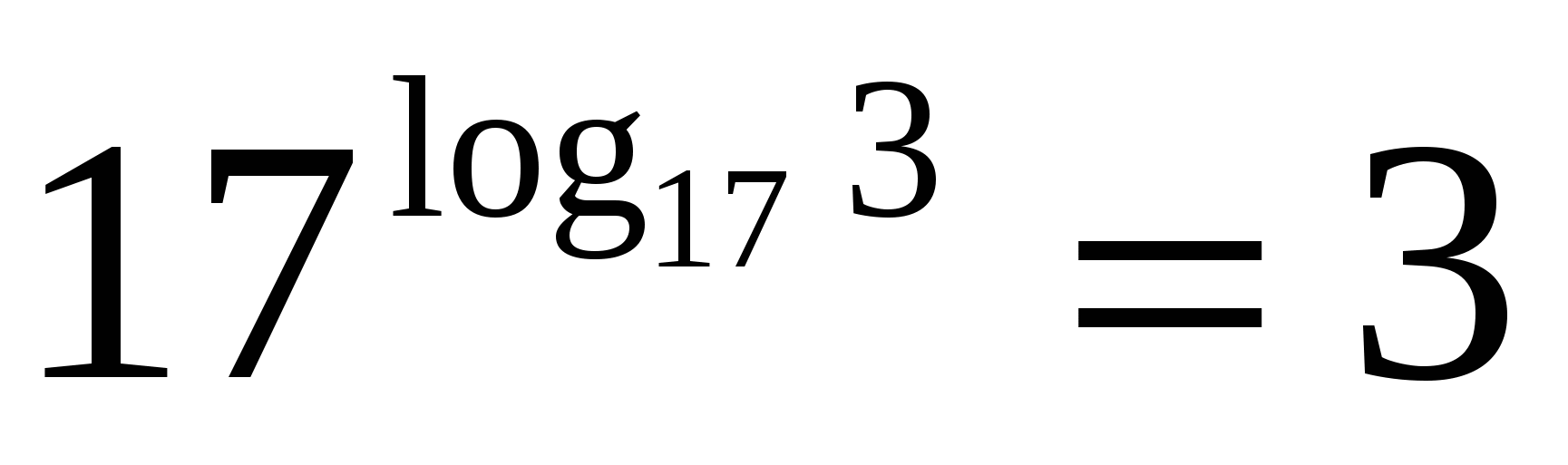

Основата на степента и основата на логаритъма са седемнадесет, което означава, че според основното логаритмично тъждество стойността на израза е три.

Да работим устно:

SCH
FIR-BELLE

ЗА долната част на втория е равна на нула цяло пет, което означава, че изразът е равен на аритметичен корен квадратен от пет.

П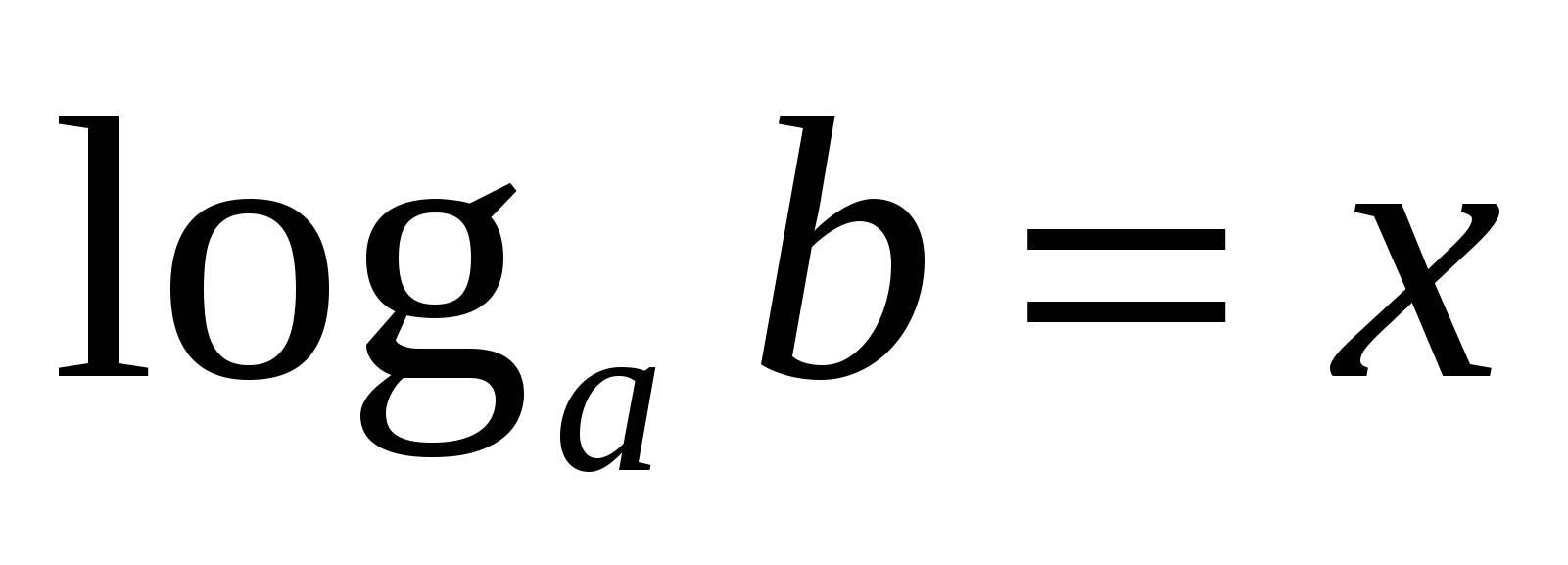

Приложение 2.

Равенство означава, че

От дефиницията на логаритъма се получават следните важни равенства:

Например:

П
Приложение 3.

Да преминем към Задачи за единен държавен изпит:

Приложение 4.

3
) Има специална нотация и име за логаритъм с основа десетдесетичен логаритъм .

Л
основен каларитъмд нареченнатурален логаритъм .

Н
например,

4) От дефиницията на логаритъм следват следните свойства. Всички свойства са формулирани и доказани само за положителни стойностипроменливи, съдържащи се под логаритмични знаци.

Логаритъм от произведението на две положителни числа към основата А равно на суматалогаритми на тези числа с една и съща основа.

ЦОР 2

например,

З
задача 1.

Задача 2.Опростете израза

IN
Нека използваме решението от предишния пример. Ние ще заменим

Моля, имайте предвид, че логаритъма е на квадрат, така че сумата трябва да бъде на квадрат. Използвайки формулата за квадрат на сумата, отваряме скобите. Нека представим подобни термини.

5) Логаритъмът на частното е равен на разликата между логаритмите на делителя и делителя.

В

Обърнете внимание на основата на степента и основата на логаритъма - те са еднакви.

ИЛИ 3

Р

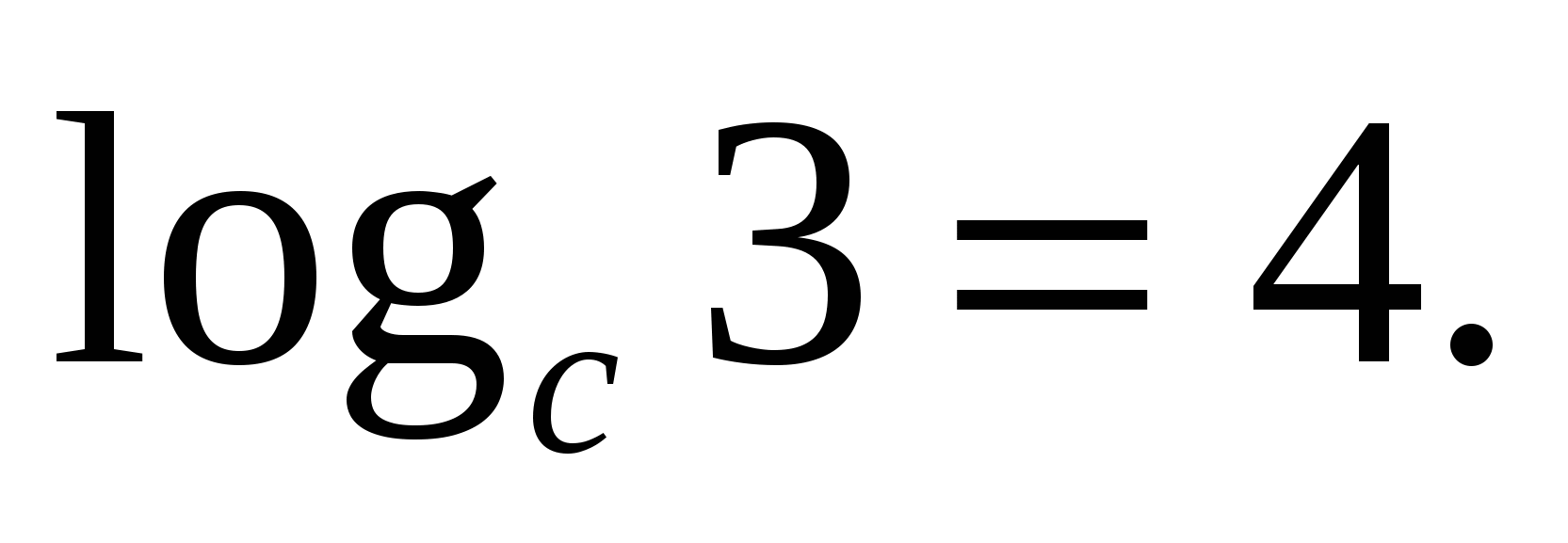Нека да разгледаме приложението на тази формула с пример:

З
задача 1.Намерете стойността на израза if

Задача 2.Намерете стойността bчрез своя логаритъм

6) Логаритъм на степен спрямо основатаА , е равно на произведението на експонентата и логаритъма с една и съща основа.

ЦОР 4

например,

З
задача 1.Изчислете дали

Нека опростим израза

Формула

наречен формула за преминаване към нова основа.

З

задача 1.Изразете с помощта на логаритъм с основа 2.

Задача 2.Изчислете

ЦОР 5

ЦОР 6

например,

З

задача 1.Изчислете

З
задача 2.Изчислете

9) Логаритмичните трансформации могат да бъдат стартирани само в случаите, когатоако помните всички свойства на логаритмите. След като ги повторим, ще разгледаме задачите за преобразуване на логаритмични изрази от другата страна.

За да преобразувате сумата или разликата на логаритмични изрази, понякога е достатъчно да използвате дефиницията на логаритъм и най-често свойствата на логаритъм от произведение или частно.

З
задача 1.Изчислете

Нека го решим по два начина.

1 начин, използвайки определението за логаритъм:

Метод 2, базиран насвойство на логаритъм от частно:

Задача 2.Намерете значението на израза

Нека първо приложим формулаталогаритъм на произведението, след това дефиницията на логаритъм.

Основната логаритмична идентичност се използва при преобразуване на изрази, съдържащи логаритъм като показател. Идеята на такива операции е да се получат равни основи на правомощията и основите на логаритъма.

Понякога е необходимо да се трансформира изражениетоот свойствата на логаритъма и от свойствата на степента, също можете лесно да преминете от една база към друга, като използвате формулата за преход. В други случаи трябва да се приложат множество свойства.

З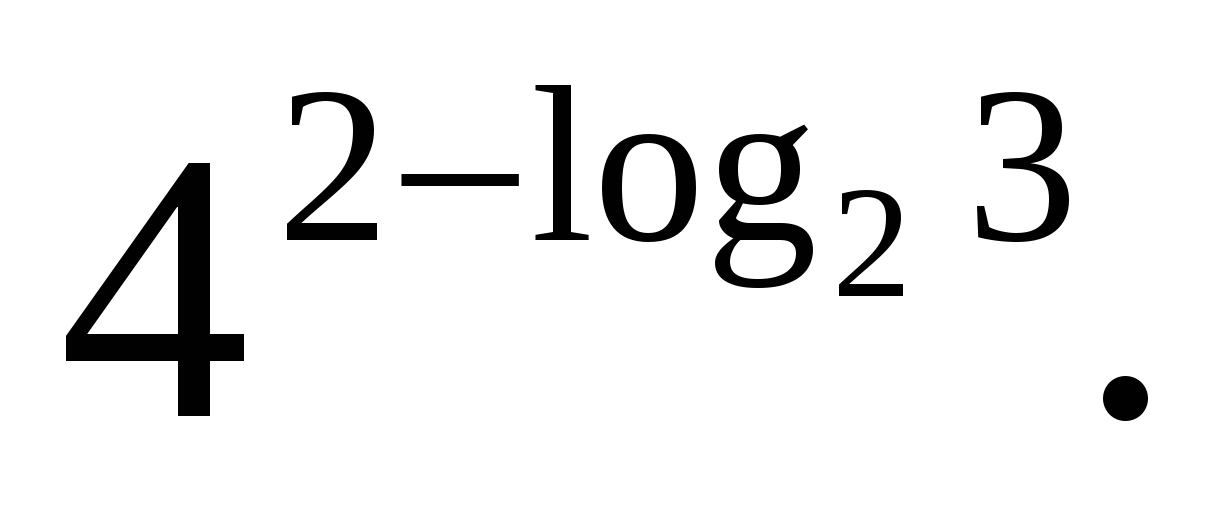
задача 3.Изчислете

З
задача 4.Намерете значението на израза

Задача 5.Намерете значението на израза

З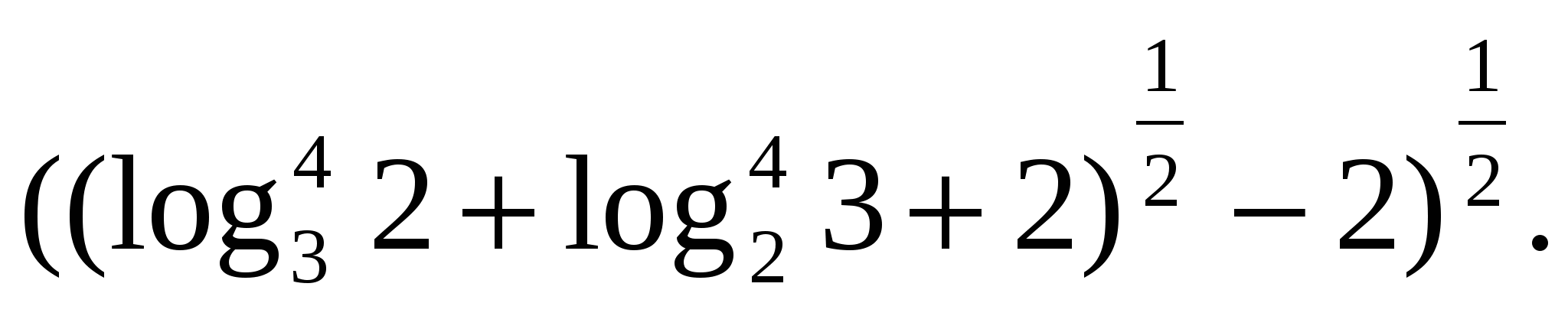
задача 6.Изразете го като разлика от логаритми

Н
Най-голямата трудност е при преобразуването на логаритмични изрази под радикала. В процеса на трансформации е необходимо да се разгледат модулите на логаритмичните изрази, за решаването на които е необходимо да се сравнят ирационални числа или рационално и ирационално число. Ще действаме последователно. Нека да разгледаме израза под вътрешния радикал.

Нека го заместим в оригиналния израз.

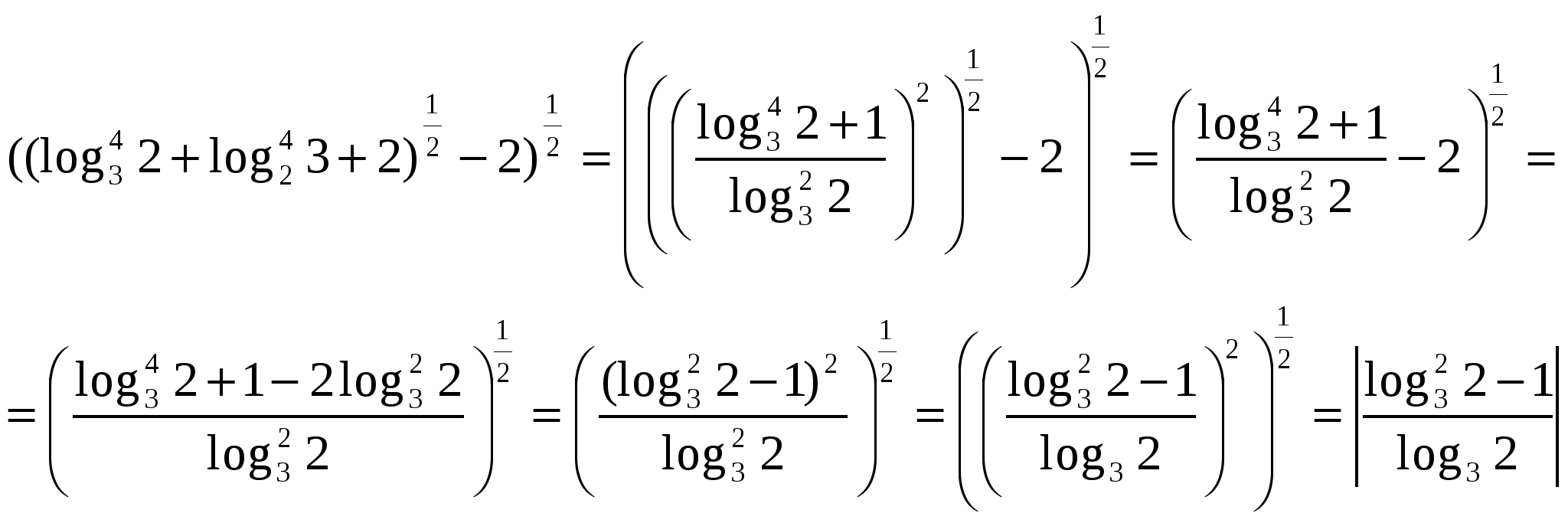Трябва да се отбележи, че преобразуването на логаритмични изрази може да се срещне и при решаване на уравнения и неравенства или изучаване на функции, поради което те могат да присъстват в имплицитна форма в задачи от групи B и C.

10) Обобщаващи въпроси:

Извиква се логаритъм при основа 10

основен логаритъм

главен логаритъм

натурален логаритъм

десетичен логаритъм

2) Какви стойности може да приеме?х в израза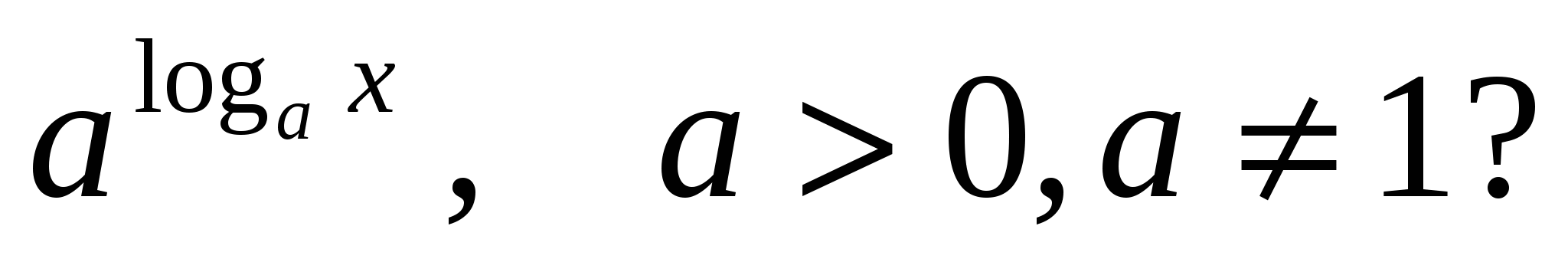

Стойността не е дефинирана

5) Дайте съотношение, което е вярно за всичких ≠ 0 .

6) Посочете правилното съотношение за формулата за преминаване към нова база.

7) Посочете правилното равенство за

11) Контролно изпитване.

Логаритмите, като всички числа, могат да се събират, изваждат и трансформират по всякакъв начин. Но тъй като логаритмите не са съвсем обикновени числа, тук има правила, които се наричат основни свойства.

Определено трябва да знаете тези правила - без тях нито един сериозен проблем не може да бъде решен. логаритмична задача. Освен това има много малко от тях - можете да научите всичко за един ден. Така че да започваме.

Събиране и изваждане на логаритми

Помислете за два логаритма с еднакви основи: log а хи дневник а г. След това те могат да се събират и изваждат и:

1. дневник а х+ дневник а г= дневник а (х · г);
2. дневник а х− дневник а г= дневник а (х : г).

И така, сумата от логаритми е равна на логаритъма от произведението, а разликата е равна на логаритъма от частното. Моля, обърнете внимание: ключова точкатук - идентични основания. Ако причините са други, тези правила не работят!

Тези формули ще ви помогнат да изчислите логаритмичен израздори когато отделните му части не се броят (вижте урока „Какво е логаритъм“). Разгледайте примерите и вижте:

Log 6 4 + log 6 9.

Тъй като логаритмите имат еднакви основи, използваме формулата за сумиране:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Задача. Намерете стойността на израза: log 2 48 − log 2 3.

Базите са еднакви, използваме формулата за разликата:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Задача. Намерете стойността на израза: log 3 135 − log 3 5.

Отново основите са същите, така че имаме:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Както можете да видите, оригиналните изрази са съставени от „лоши“ логаритми, които не се изчисляват отделно. Но след трансформациите се получават напълно нормални числа. Много от тях са изградени върху този факт тестове. Да, изрази, подобни на тестове, се предлагат напълно сериозно (понякога почти без промени) на Единния държавен изпит.

Извличане на показателя от логаритъма

Сега нека усложним малко задачата. Ами ако основата или аргументът на логаритъм е степен? Тогава показателят на тази степен може да бъде изваден от знака на логаритъма съгласно следните правила:

Лесно се вижда, че последното правило следва първите две. Но все пак е по-добре да го запомните - в някои случаи това значително ще намали количеството на изчисленията.

Разбира се, всички тези правила имат смисъл, ако се спазва ODZ на логаритъма: а > 0, а ≠ 1, х> 0. И още нещо: научете се да прилагате всички формули не само отляво надясно, но и обратно, т.е. Можете да въведете числата преди знака за логаритъм в самия логаритъм. Това е, което най-често се изисква.

Задача. Намерете стойността на израза: log 7 49 6 .

Нека се отървем от степента в аргумента, използвайки първата формула:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Задача. Намерете значението на израза:

[Надпис към снимката]

Забележете, че знаменателят съдържа логаритъм, чиято основа и аргумент са точни степени: 16 = 2 4 ; 49 = 7 2. Ние имаме:

[Надпис към снимката]

Мисля, че последният пример изисква известно пояснение. Къде изчезнаха логаритмите? До последния момент работим само със знаменателя. Представихме основата и аргумента на логаритъма, който стои там под формата на степени и извадихме показателите - получихме "триетажна" дроб.

Сега нека разгледаме основната фракция. Числителят и знаменателят съдържат едно и също число: log 2 7. Тъй като log 2 7 ≠ 0, можем да намалим дробта - 2/4 ще остане в знаменателя. Според правилата на аритметиката четворката може да се прехвърли в числителя, което и беше направено. Резултатът беше отговорът: 2.

Преход към нова основа

Говорейки за правилата за събиране и изваждане на логаритми, специално подчертах, че те работят само с еднакви основи. Ами ако причините са различни? Ами ако не са точни степени на едно и също число?

Формулите за преход към нова основа идват на помощ. Нека ги формулираме под формата на теорема:

Нека логаритъмът е даден а х. След това за произволен номер cтакова, че c> 0 и c≠ 1 равенството е вярно:

[Надпис към снимката]

По-специално, ако поставим c = х, получаваме:

[Надпис към снимката]

От втората формула следва, че основата и аргументът на логаритъма могат да се разменят, но в този случай целият израз се „обръща“, т.е. логаритъма се появява в знаменателя.

Тези формули рядко се срещат в обикновени числови изрази. Възможно е да се оцени колко са удобни само при решаване на логаритмични уравнения и неравенства.

Има обаче проблеми, които изобщо не могат да бъдат решени, освен чрез преминаване към нова основа. Нека да разгледаме няколко от тях:

Задача. Намерете стойността на израза: log 5 16 log 2 25.

Обърнете внимание, че аргументите на двата логаритма съдържат точни степени. Нека извадим индикаторите: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Сега нека "обърнем" втория логаритъм:

[Надпис към снимката]

Тъй като продуктът не се променя при пренареждане на множителите, ние спокойно умножихме четири и две и след това се справихме с логаритмите.

Задача. Намерете стойността на израза: log 9 100 lg 3.

Основата и аргументът на първия логаритъм са точни степени. Нека запишем това и да се отървем от индикаторите:

[Надпис към снимката]

Сега нека се отървем от десетичния логаритъм, като преминем към нова основа:

[Надпис към снимката]

Основно логаритмично тъждество

Често в процеса на решаване е необходимо да се представи число като логаритъм на дадена основа. В този случай ще ни помогнат следните формули:

В първия случай броят пстава показател за степента на позиция в спора. Номер пможе да бъде абсолютно всичко, защото това е просто логаритъм.

Втората формула всъщност е перифразирана дефиниция. Това се нарича: основна логаритмична идентичност.

Всъщност какво ще се случи, ако броят bповдигнете до такава степен, че числото bна тази степен дава числото а? Точно така: получавате същото число а. Прочетете внимателно този параграф отново - много хора се забиват в него.

Подобно на формулите за преминаване към нова база, основното логаритмично тъждество понякога е единственото възможно решение.

Задача. Намерете значението на израза:

[Надпис към снимката]

Обърнете внимание, че log 25 64 = log 5 8 - ние просто взехме квадрат от основата и аргумента на логаритъма. Като вземем предвид правилата за умножение на степени с една и съща основа, получаваме:

[Надпис към снимката]

Ако някой не знае, това беше истинска задача от Единния държавен изпит :)

Логаритмична единица и логаритмична нула

В заключение ще дам две тъждества, които трудно могат да бъдат наречени свойства - по-скоро те са следствия от дефиницията на логаритъма. Те постоянно се появяват в проблеми и, изненадващо, създават проблеми дори за „напреднали“ ученици.

1. дневник а а= 1 е логаритмична единица. Запомнете веднъж завинаги: логаритъм по произволна основа аот същата тази основа е равно на едно.
2. дневник а 1 = 0 е логаритмична нула. База аможе да бъде всичко, но ако аргументът съдържа единица, логаритъма е равен на нула! защото а 0 = 1 е пряко следствие от определението.

Това са всички имоти. Не забравяйте да се упражнявате да ги прилагате на практика! Изтеглете измамника в началото на урока, разпечатайте го и решете задачите.

Поддържането на вашата поверителност е важно за нас. Поради тази причина разработихме Политика за поверителност, която описва как използваме и съхраняваме вашата информация. Моля, прегледайте нашите практики за поверителност и ни уведомете, ако имате въпроси.

Събиране и използване на лична информация

Личната информация се отнася до данни, които могат да бъдат използвани за идентифициране или контакт с конкретно лице.

Може да бъдете помолени да предоставите вашата лична информация по всяко време, когато се свържете с нас.

По-долу са дадени някои примери за видовете лична информация, която можем да събираме и как можем да използваме тази информация.

Каква лична информация събираме:

• Когато подадете заявка на сайта, ние може да съберем различна информация, включително вашето име, телефонен номер, адрес имейли т.н.

Как използваме вашата лична информация:

• Събрани от нас лична информацияни позволява да се свързваме с вас и да ви информираме за уникални оферти, промоции и други събития и предстоящи събития.
• От време на време може да използваме вашата лична информация, за да изпращаме важни известия и съобщения.
• Може също така да използваме лична информация за вътрешни цели, като например извършване на одити, анализ на данни и различни изследвания, за да подобрим услугите, които предоставяме, и да ви предоставим препоръки относно нашите услуги.
• Ако участвате в теглене на награди, конкурс или подобна промоция, ние може да използваме предоставената от вас информация за администриране на такива програми.

Разкриване на информация на трети лица

Ние не разкриваме информацията, получена от вас, на трети страни.

Изключения:

• При необходимост - в съответствие със закона, съдебната процедура, съдебното производство и/или въз основа на публични искания или искания от държавни агенциина територията на Руската федерация - разкрийте вашата лична информация. Може също така да разкрием информация за вас, ако преценим, че такова разкриване е необходимо или подходящо за целите на сигурността, правоприлагането или други обществено значими цели.
• В случай на реорганизация, сливане или продажба, можем да прехвърлим личната информация, която събираме, на съответната трета страна приемник.

Защита на личната информация

Ние вземаме предпазни мерки – включително административни, технически и физически – за да защитим вашата лична информация от загуба, кражба и злоупотреба, както и неоторизиран достъп, разкриване, промяна и унищожаване.

Зачитане на вашата поверителност на фирмено ниво

За да гарантираме, че вашата лична информация е защитена, ние съобщаваме стандартите за поверителност и сигурност на нашите служители и стриктно прилагаме практиките за поверителност.

Инструкции

Напишете дадения логаритмичен израз. Ако изразът използва логаритъм от 10, тогава записът му се съкращава и изглежда така: lg b е десетичният логаритъм. Ако основата на логаритъма е числото e, тогава напишете израза: ln b – натурален логаритъм. Разбираемо е, че резултатът от any е степента, на която трябва да се повдигне основното число, за да се получи числото b.

Когато намирате сумата на две функции, просто трябва да ги разграничите една по една и да съберете резултатите: (u+v)" = u"+v";

Когато намирате производната на произведението на две функции, е необходимо да умножите производната на първата функция по втората и да добавите производната на втората функция, умножена по първата функция: (u*v)" = u"*v +v"*u;

За да се намери производната на частното на две функции, е необходимо да се извади от произведението на производната на дивидента, умножено по функцията делител, произведението на производната на делителя, умножено по функцията на делителя, и да се раздели всичко това чрез функцията делител на квадрат. (u/v)" = (u"*v-v"*u)/v^2;

Ако се даде сложна функция, тогава е необходимо да се умножи производната на вътрешната функция и производната на външната. Нека y=u(v(x)), тогава y"(x)=y"(u)*v"(x).

Използвайки резултатите, получени по-горе, можете да разграничите почти всяка функция. Така че нека да разгледаме няколко примера:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *x));
Има и проблеми, свързани с изчисляването на производната в точка. Нека е дадена функцията y=e^(x^2+6x+5), трябва да намерите стойността на функцията в точката x=1.
1) Намерете производната на функцията: y"=e^(x^2-6x+5)*(2*x +6).

2) Изчислете стойността на функцията в дадена точка y"(1)=8*e^0=8

Видео по темата

Полезен съвет

Научете таблицата на елементарните производни. Това значително ще спести време.

източници:

• производна на константа

И така, каква е разликата между рационално уравнениеот рационалното? Ако неизвестната променлива е под знака корен квадратен, тогава уравнението се счита за ирационално.

Инструкции

Основният метод за решаване на такива уравнения е методът за конструиране на двете страни уравненияв квадрат. Въпреки това. това е естествено, първото нещо, което трябва да направите, е да се отървете от знака. Този метод не е технически труден, но понякога може да доведе до проблеми. Например, уравнението е v(2x-5)=v(4x-7). Като повдигнете двете страни на квадрат, получавате 2x-5=4x-7. Решаването на такова уравнение не е трудно; х=1. Но номер 1 няма да бъде даден уравнения. защо Заместете едно в уравнението вместо стойността на x и дясната и лявата страна ще съдържат изрази, които нямат смисъл, т.е. Тази стойност не е валидна за квадратен корен. Следователно 1 е външен корен и следователно дадено уравнениеняма корени.

И така, ирационално уравнение се решава с помощта на метода на повдигане на квадрат на двете му страни. И след като се реши уравнението, е необходимо да се отрежат външни корени. За да направите това, заменете намерените корени в оригиналното уравнение.

Помислете за друг.
2х+vх-3=0
Разбира се, това уравнение може да бъде решено с помощта на същото уравнение като предишното. Преместване на съединения уравнения, които нямат квадратен корен, надясно и след това използвайте метода на повдигане на квадрат. решаване на полученото рационално уравнение и корени. Но и друг, по-елегантен. Въведете нова променлива; vх=y. Съответно ще получите уравнение от формата 2y2+y-3=0. Тоест обичайното квадратно уравнение. Намерете неговите корени; y1=1 и y2=-3/2. След това решете две уравнения vх=1; vх=-3/2. Второто уравнение няма корени; от първото намираме, че x=1. Не забравяйте да проверите корените.

Разрешаването на идентичности е доста просто. За да направите това, е необходимо да извършите идентични трансформации, докато се постигне поставената цел. Така с помощта на прости аритметични действия поставеният проблем ще бъде решен.

Ще ви трябва

• - хартия;
• - писалка.

Инструкции

Най-простите от тези трансформации са алгебричните съкратени умножения (като квадрат на сумата (разликата), разликата на квадратите, сумата (разликата), кубът на сумата (разликата)). Освен това има много и тригонометрични формули, които по същество са едни и същи самоличности.

Наистина, квадратът на сбора от два члена е равен на квадрата на първия плюс два пъти произведението на първия по втория и плюс квадрата на втория, тоест (a+b)^2= (a+ b)(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Опростете и двете

Общи принципи на решението

Повторете от учебник по математически анализ или висша математика какво е определен интеграл. Както е известно, решението определен интегралима функция, чиято производна дава интегранд. Тази функция се нарича антипроизводна. Въз основа на този принцип се конструират основните интеграли.
Определете според вида на интегранта кой от табличните интеграли е подходящ в този случай. Не винаги е възможно да се определи това веднага. Често табличната форма става забележима само след няколко трансформации за опростяване на интегралната функция.

Метод за заместване на променливи

Ако функцията интегранд е тригонометрична функция, чийто аргумент съдържа някакъв полином, опитайте да използвате метода за заместване на променлива. За да направите това, заменете полинома в аргумента на интегранта с нова променлива. Въз основа на връзката между новите и старите променливи, определете новите граници на интегриране. Като диференцирате този израз, намерете новия диференциал в . Така че ще получите нов обликна предишния интеграл, близък или дори съответстващ на всеки табличен.

Решаване на интеграли от втори род

Ако интегралът е интеграл от втори вид, векторна форма на интегранта, тогава ще трябва да използвате правилата за преход от тези интеграли към скаларни. Едно такова правило е отношението на Остроградски-Гаус. Този закон ни позволява да преминем от роторния поток на определена векторна функция към тройния интеграл върху дивергенцията на дадено векторно поле.

Замяна на интеграционни граници

След намиране на антипроизводното е необходимо да се заменят границите на интегриране. Първо, заместете стойността на горната граница в израза за антипроизводното. Ще получите някакъв номер. След това извадете от полученото число друго число, получено от долната граница в антипроизводното. Ако една от границите на интегриране е безкрайност, тогава при заместването й в антипроизводната функция е необходимо да отидете до границата и да намерите към какво клони изразът.
Ако интегралът е двуизмерен или триизмерен, тогава ще трябва да представите границите на интеграцията геометрично, за да разберете как да оцените интеграла. Наистина, в случая на, да речем, триизмерен интеграл, границите на интегриране могат да бъдат цели равнини, които ограничават обема, който се интегрира.

При преобразуване на изрази с логаритми изброените равенства се използват както отдясно наляво, така и отляво надясно.

Струва си да се отбележи, че не е необходимо да запаметявате последствията от свойствата: когато извършвате трансформации, можете да се справите с основните свойства на логаритмите и други факти (например факта, че за b≥0), от които следват съответните последствия. " Страничен ефект„Този ​​подход се проявява само в това, че решението ще бъде малко по-дълго. Например, за да се направи без последствието, което се изразява с формулата , и започвайки само от основните свойства на логаритмите, ще трябва да извършите верига от трансформации следния тип: .

Същото може да се каже и за последното свойство от горния списък, на което отговаря формулата , тъй като следва и от основните свойства на логаритмите. Основното нещо, което трябва да разберете, е, че винаги е възможно степента на положително число с логаритъм в степента да размени основата на степента и числото под знака на логаритъма. За да бъдем честни, отбелязваме, че примерите, предполагащи изпълнението на трансформации от този вид, са рядкост на практика. По-долу в текста ще дадем няколко примера.

Преобразуване на числови изрази с логаритми

Спомнихме си свойствата на логаритмите, сега е време да научим как да ги прилагаме на практика за трансформиране на изрази. Естествено е да започнете с преобразуване на числови изрази, а не на изрази с променливи, тъй като те са по-удобни и по-лесни за научаване на основите. Това е, което ще направим и ще започнем с много прости примери, за да научите как да изберете желаното свойство на логаритъма, но ние постепенно ще усложняваме примерите, до момента, в който за получаване на крайния резултат ще е необходимо да приложите няколко свойства подред.

Избор на желаното свойство на логаритмите

Има много свойства на логаритмите и е ясно, че трябва да можете да изберете подходящото, което в конкретния случай ще доведе до желания резултат. Обикновено това не е трудно да се направи чрез сравняване на вида на преобразувания логаритъм или израз с типовете лява и дясна част на формули, изразяващи свойствата на логаритмите. Ако лявата или дясната страна на една от формулите съвпада с даден логаритъм или израз, тогава най-вероятно това свойство трябва да се използва по време на трансформацията. Следните примери ясно показват това.

Нека започнем с примери за преобразуване на изрази, използвайки дефиницията на логаритъм, която съответства на формулата a log a b =b, a>0, a≠1, b>0.

Пример.

Изчислете, ако е възможно: a) 5 log 5 4, b) 10 log(1+2·π), c) , г) 2 log 2 (−7) , д) .

Решение.

В примера под буква а) ясно се вижда структурата a log a b, където a=5, b=4. Тези числа отговарят на условията a>0, a≠1, b>0, така че можете спокойно да използвате равенството a log a b =b. Имаме 5 log 5 4=4 .

b) Тук a=10, b=1+2·π, условията a>0, a≠1, b>0 са изпълнени. В този случай се изпълнява равенството 10 log(1+2·π) =1+2·π.

в) И в този пример имаме работа със степен от формата a log a b, където и b=ln15. И така .

Въпреки че принадлежи към същия тип a log a b (тук a=2, b=−7), изразът под буквата g) не може да бъде преобразуван с помощта на формулата a log a b =b. Причината е, че е безсмислено, тъй като съдържа отрицателно число под знака на логаритъма. Освен това числото b=−7 не отговаря на условието b>0, което прави невъзможно прибягването до формулата a log a b =b, тъй като тя изисква изпълнението на условията a>0, a≠1, b> 0. Така че не можем да говорим за изчисляване на стойността на 2 log 2 (−7) . В този случай писането на 2 log 2 (−7) =−7 би било грешка.

По същия начин в примера под буква д) е невъзможно да се даде решение на формата , тъй като оригиналният израз няма смисъл.

отговор:

a) 5 log 5 4 =4, b) 10 log(1+2·π) =1+2·π, c) , г), д) изразите нямат смисъл.

Трансформацията често е полезна, при която положително число е представено като степен на някакво положително и неединствено число с логаритъм в степента. Базира се на същата дефиниция на логаритъма a log a b =b, a>0, a≠1, b>0, но формулата се прилага отдясно наляво, тоест във формата b=a log a b . Например 3=e ln3 или 5=5 log 5 5 .

Нека да преминем към използването на свойствата на логаритмите за трансформиране на изрази.

Пример.

Намерете стойността на израза: a) log −2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, f) log1, g) log 3,75 1, h) log 5 π 7 1 .

Решение.

В примерите под букви а), б) и в) са дадени изразите log −2 1, log 1 1, log 0 1, които нямат смисъл, тъй като основата на логаритъма не трябва да съдържа отрицателно число, нула или едно, защото сме дефинирали логаритъм само за основа, която е положителна и различна от единица. Следователно в примери а) - в) не може да става дума за намиране на смисъла на израза.

Във всички останали задачи, очевидно, основите на логаритмите съдържат съответно положителни и неединични числа 7, e, 10, 3,75 и 5·π 7, а под знаците на логаритмите навсякъде има единици. И знаем свойството на логаритъма от единица: log a 1=0 за всяко a>0, a≠1. По този начин стойностите на изразите b) – e) са равни на нула.

отговор:

a), b), c) изразите нямат смисъл, d) log 7 1=0, e) ln1=0, f) log1=0, g) log 3,75 1=0, h) log 5 e 7 1= 0 .

Пример.

Изчислете: а) , б) lne , в) lg10 , г) log 5 π 3 −2 (5 π 3 −2), д) log −3 (−3) , f) log 1 1 .

Решение.

Ясно е, че трябва да използваме свойството на логаритъма на основата, което съответства на формулата log a a=1 за a>0, a≠1. Наистина в задачите под всички букви числото под знака на логаритъма съвпада с основата му. Затова бих искал веднага да кажа, че стойността на всеки от дадените изрази е 1. Не бива обаче да бързате със заключенията: в задачите под букви а) - г) стойностите на изразите наистина са равни на единица, а в задачи д) и е) оригиналните изрази нямат смисъл, така че не може да се каже, че стойностите на тези изрази са равни на 1.

отговор:

а) , б) lne=1 , в) lg10=1 , г) log 5 π 3 −2 (5 π 3 −2)=1, д), е) изразите нямат смисъл.

Пример.

Намерете стойността: а) log 3 3 11, б) , в), г) log −10 (−10) 6 .

Решение.

Очевидно под знаците на логаритмите има някои степени на основата. Въз основа на това разбираме, че тук ще ни трябва свойството на степента на основата: log a a p =p, където a>0, a≠1 и p е всяко реално число. Като вземем това предвид, имаме следните резултати: а) log 3 3 11 =11, б) , V) . Може ли да се напише подобно равенство за примера под буква d) от вида log −10 (−10) 6 =6? Не, не можете, защото изразът log −10 (−10) 6 няма смисъл.

отговор:

а) log 3 3 11 =11, б) , V) , г) изразът няма смисъл.

Пример.

Представете израза като сбор или разлика от логаритми, като използвате една и съща основа: а) , b) , c) log((−5)·(−12)) .

Решение.

а) Под знака на логаритъма стои произведение и знаем свойството на логаритъма на произведението log a (x·y)=log a x+log a y, a>0, a≠1, x>0 , y>0. В нашия случай числото в основата на логаритъма и числата в произведението са положителни, т.е. те отговарят на условията на избраното свойство, следователно можем безопасно да го приложим: .

б) Тук използваме свойството на частния логаритъм, където a>0, a≠1, x>0, y>0. В нашия случай основата на логаритъма е положително число e, числителят и знаменателят π са положителни, което означава, че отговарят на условията на свойството, така че имаме право да използваме избраната формула: .

c) Първо, отбележете, че изразът log((−5)·(−12)) има смисъл. Но в същото време за него нямаме право да приложим формулата за логаритъм на произведението log a (x y)=log a x+log a y, a>0, a≠1, x>0, y >0, тъй като числата са −5 и −12 – отрицателни и не отговарят на условията x>0, y>0. Тоест не можете да извършите такава трансформация: log((−5)·(−12))=log(−5)+log(−12). И така, какво трябва да направим? В такива случаи оригиналният израз се нуждае от предварителна трансформация, за да се избегнат отрицателни числа. За подобни случаи на преобразуване на изрази с отрицателни числапод знака на логаритъма, ще говорим подробно в един от тях, но засега ще дадем решение на този пример, който е ясен предварително и без обяснение: log((−5)·(−12))=log(5·12)=log5+lg12.

отговор:

а) , б) , в) log((−5)·(−12))=log5+lg12.

Пример.

Опростете израза: а) log 3 0,25+log 3 16+log 3 0,5, б) .

Решение.

Тук ще ни помогнат всички същите свойства на логаритъма на произведението и логаритъма на частното, които използвахме в предишните примери, само сега ще ги приложим отдясно наляво. Тоест, трансформираме сумата от логаритми в логаритъм от произведението и разликата от логаритми в логаритъм от частното. Имаме
а) log 3 0,25+log 3 16+log 3 0,5=log 3 (0,25 16 0,5)=log 3 2.
б) .

отговор:

а) log 3 0,25+log 3 16+log 3 0,5=log 3 2, б) .

Пример.

Отървете се от степента под знака на логаритъма: а) log 0,7 5 11, б) , в) log 3 (−5) 6 .

Решение.

Лесно се вижда, че имаме работа с изрази от формата log a b p . Съответното свойство на логаритъма има формата log a b p =p·log a b, където a>0, a≠1, b>0, p е всяко реално число. Тоест, ако условията a>0, a≠1, b>0 са изпълнени, от логаритъма на степенния log a b p можем да преминем към произведението p·log a b. Нека извършим тази трансформация с дадените изрази.

а) В този случай a=0,7, b=5 и p=11. Значи log 0,7 5 11 =11 · log 0,7 5.

б) Тук са изпълнени условията a>0, a≠1, b>0. Ето защо

в) Изразът log 3 (−5) 6 има същата структура log a b p , a=3 , b=−5 , p=6 . Но за b условието b>0 не е изпълнено, което прави невъзможно използването на формулата log a b p =p·log a b . И какво, не можете да се справите със задачата? Възможно е, но е необходима предварителна трансформация на израза, която ще разгледаме подробно по-долу в параграфа под заглавието. Решението ще бъде така: log 3 (−5) 6 =log 3 5 6 =6 log 3 5.

отговор:

а) log 0,7 5 11 =11 log 0,7 5 ,
б)
в) log 3 (−5) 6 =6 log 3 5.

Доста често, когато се извършват трансформации, формулата за логаритъм на степен трябва да се приложи отдясно наляво във формата p·log a b=log a b p (същите условия трябва да бъдат изпълнени за a, b и p). Например, 3·ln5=ln5 3 и log2·log 2 3=log 2 3 lg2.

Пример.

а) Изчислете стойността на log 2 5, ако е известно, че log2≈0,3010 и log5≈0,6990. б) Изразете дробта като логаритъм при основа 3.

Решение.

а) Формулата за преход към нова логаритъмна база ни позволява да представим този логаритъм като съотношение на десетични логаритми, чиито стойности са ни известни: . Остава само да извършим изчисленията, които имаме .

б) Тук е достатъчно да използвате формулата за преместване към нова база и да я приложите отдясно наляво, тоест във формата . получаваме .

отговор:

а) log 2 5≈2,3223, б) .

На този етап разгледахме доста подробно преобразуването на най-простите изрази, използвайки основните свойства на логаритмите и дефиницията на логаритъм. В тези примери трябваше да приложим едно свойство и нищо повече. Сега с чиста съвест можете да преминете към примери, чиято трансформация изисква използването на няколко свойства на логаритми и други допълнителни трансформации. Ще се занимаем с тях в следващия параграф. Но преди това нека разгледаме накратко примери за прилагане на следствия от основните свойства на логаритмите.

Пример.

а) Отървете се от корена под знака на логаритъма. б) Преобразувайте дробта в логаритъм с основа 5. в) Освободете се от степени под знака на логаритъма и в неговата основа. г) Изчислете стойността на израза . д) Заменете израза със степен с основа 3.

Решение.

а) Ако си припомним следствието от свойството логаритъм на степента , тогава можете веднага да дадете отговора: .

б) Тук използваме формулата от дясно на ляво имаме .

в) В този случай формулата води до резултата . получаваме .

г) И тук е достатъчно да приложим следствието, на което отговаря формулата . И така .

д) Свойство на логаритъма ни позволява да постигнем желания резултат: .

отговор:

а) . б) . V) . G) . г) .

Последователно прилагане на няколко свойства

Реалните задачи за преобразуване на изрази, използващи свойствата на логаритмите, обикновено са по-сложни от тези, които разгледахме в предишния параграф. При тях, като правило, резултатът не се получава на една стъпка, а решението вече се състои в последователно прилагане на едно свойство след друго, заедно с допълнителни идентични трансформации, като отваряне на скоби, привеждане на подобни членове, намаляване на дроби и т.н. . Така че нека се доближим до такива примери. В това няма нищо сложно, основното е да действате внимателно и последователно, като спазвате реда на действията.

Пример.

Изчислете стойността на израз (log 3 15−log 3 5) 7 log 7 5.

Решение.

Разликата между логаритмите в скоби, според свойството на частния логаритъм, може да бъде заменена с логаритъм log 3 (15:5) и след това да се изчисли неговата стойност log 3 (15:5)=log 3 3=1. И стойността на израза 7 log 7 5 по дефиниция на логаритъм е равна на 5. Замествайки тези резултати в оригиналния израз, получаваме (log 3 15−log 3 5) 7 log 7 5 =1 5=5.

Ето решение без обяснение:
(log 3 15−log 3 5) 7 log 7 5 =log 3 (15:5) 5=
=log 3 3·5=1·5=5 .

отговор:

(log 3 15−log 3 5) 7 log 7 5 =5.

Пример.

Каква е стойността на числовия израз log 3 log 2 2 3 −1?

Решение.

Първо трансформираме логаритъма под знака за логаритъм, използвайки формулата за логаритъм на степен: log 2 2 3 =3. Така, log 3 log 2 2 3 =log 3 3 и след това log 3 3=1. Така че log 3 log 2 2 3 −1=1−1=0 .

отговор:

log 3 log 2 2 3 −1=0 .

Пример.

Опростете израза.

Решение.

Формулата за преминаване към нова основа на логаритъм позволява съотношението на логаритмите към една основа да бъде представено като log 3 5. В този случай оригиналният израз ще приеме формата . По дефиниция на логаритъма 3 log 3 5 =5, т.е , а стойността на получения израз, по силата на същата дефиниция на логаритъма, е равна на две.

тук кратка версиярешения, които обикновено се дават: .

отговор:

.

За да преминете плавно към информацията в следващия параграф, нека да разгледаме изразите 5 2+log 5 3 и log0.01. Тяхната структура не отговаря на нито едно от свойствата на логаритмите. И така, какво се случва, те не могат да бъдат преобразувани с помощта на свойствата на логаритмите? Възможно е, ако извършите предварителни трансформации, които подготвят тези изрази за прилагане на свойствата на логаритмите. И така 5 2+log 5 3 =5 2 5 log 5 3 =25 3=75, и log0.01=log10 −2 =−2. След това ще разгледаме подробно как се прави това. подобен препаратизрази.

Подготовка на изрази за използване на свойствата на логаритмите

Логаритмите в израза, който се преобразува, много често се различават в структурата на нотацията от лявата и дясната част на формулите, които съответстват на свойствата на логаритмите. Но не по-рядко преобразуването на тези изрази включва използването на свойствата на логаритмите: за да ги използвате, трябва само предварителна подготовка. И тази подготовка се състои в извършване на определени идентични трансформации, които привеждат логаритмите във форма, удобна за прилагане на свойствата.

За да бъдем честни, отбелязваме, че почти всяка трансформация на изрази може да действа като предварителни трансформации, от баналното намаляване на подобни термини до използването на тригонометрични формули. Това е разбираемо, тъй като преобразуваните изрази могат да съдържат всякакви математически обекти: скоби, модули, дроби, корени, степени и т.н. Следователно, човек трябва да е готов да извърши всяка необходима трансформация, за да може по-нататък да се възползва от свойствата на логаритмите.

Нека кажем веднага, че на този етап не си поставяме задачата да класифицираме и анализираме всички възможни предварителни трансформации, които биха ни позволили впоследствие да приложим свойствата на логаритмите или дефиницията на логаритъм. Тук ще се спрем само на четири от тях, които са най-характерни и най-често срещани в практиката.

И сега за всеки от тях по-подробно, след което, в рамките на нашата тема, всичко, което остава, е да разберем трансформацията на изрази с променливи под знаците на логаритмите.

Идентификация на степените под знака на логаритъма и в основата му

Нека започнем веднага с пример. Нека имаме логаритъм. Очевидно в тази форма неговата структура не е благоприятна за използване на свойствата на логаритмите. Възможно ли е по някакъв начин да се трансформира този израз, за ​​да се опрости и дори по-добре да се изчисли стойността му? За да отговорим на този въпрос, нека разгледаме по-подробно числата 81 и 1/9 в контекста на нашия пример. Тук е лесно да се забележи, че тези числа могат да бъдат представени като степен на 3, наистина, 81 = 3 4 и 1/9 = 3 −2. В този случай оригиналният логаритъм се представя във формуляра и става възможно прилагането на формулата . така че .

Анализът на анализирания пример поражда следната мисъл: ако е възможно, можете да опитате да изолирате степента под знака на логаритъма и в неговата основа, за да приложите свойството на логаритъма на степента или неговите последствия. Остава само да разберем как да разграничим тези степени. Нека да дадем някои препоръки по този въпрос.

Понякога е съвсем очевидно, че числото под знака на логаритъма и/или в основата му представлява някаква цяло число, както в примера, обсъден по-горе. Почти непрекъснато се налага да боравим със степени на две, които са добре познати: 4=2 2, 8=2 3, 16=2 4, 32=2 5, 64=2 6, 128=2 7, 256=2 8 , 512= 2 9, 1024=2 10. Същото може да се каже и за степените на три: 9 = 3 2, 27 = 3 3, 81 = 3 4, 243 = 3 5, ... Като цяло няма да навреди, ако имате пред очите си таблица на градусите естествени числа в рамките на дузина. Също така не е трудно да се работи с цели степени на десет, сто, хиляда и т.н.

Пример.

Изчислете стойността или опростете израза: a) log 6 216, b) , c) log 0,000001 0,001.

Решение.

а) Очевидно 216=6 3, така че log 6 216=log 6 6 3 =3.

б) Таблицата на степените на естествените числа ви позволява да представите числата 343 и 1/243 съответно като степени 7 3 и 3 −4. Следователно е възможно следното преобразуване на даден логаритъм:

в) Тъй като 0,000001=10 −6 и 0,001=10 −3, тогава log 0,000001 0,001=log 10 −6 10 −3 =(−3)/(−6)=1/2.

отговор:

а) log 6 216=3, б) , c) log 0,000001 0,001=1/2.

В повече трудни случаиза да се разграничат степените на числата, трябва да се прибегне до .

Пример.

Преобразувайте израза в повече прост изглед log 3 648 log 2 3 .

Решение.

Нека да разгледаме какво представлява факторизирането на 648:

Тоест 648=2 3 ·3 4. по този начин log 3 648 log 2 3=log 3 (2 3 3 4) log 2 3.

Сега трансформираме логаритъма на произведението в сумата от логаритми, след което прилагаме свойствата на логаритъма на степента:
log 3 (2 3 3 4)log 2 3=(log 3 2 3 +log 3 3 4)log 2 3=
=(3·log 3 2+4)·log 2 3 .

По силата на следствие от свойството на логаритъм на степента, което съответства на формулата , произведението log32·log23 е произведение на , и, както е известно, е равно на едно. Като вземем това предвид, получаваме 3 log 3 2 log 2 3+4 log 2 3=3 1+4 log 2 3=3+4 log 2 3.

отговор:

log 3 648 log 2 3=3+4 log 2 3.

Много често изразите под знака на логаритъма и в основата му представляват произведения или съотношения на корени и/или степени на някои числа, например, , . Такива изрази могат да бъдат изразени като правомощия. За да направите това, се прави преход от корени към правомощия и се използват и . Тези трансформации позволяват да се изолират степените под знака на логаритъма и в неговата основа и след това да се приложат свойствата на логаритмите.

Пример.

Изчислете: а) , б) .

Решение.

а) Изразът в основата на логаритъма е произведение на степени с еднакви основи по съответното свойство на степените, които имаме; 5 2 ·5 −0,5 ·5 −1 =5 2−0,5−1 =5 0,5.

Сега нека трансформираме дроба под знака на логаритъма: ще преминем от корена към степента, след което ще използваме свойството на съотношението на мощностите с еднакви основи: .

Остава да замените получените резултати в оригиналния израз, използвайте формулата и завършете трансформацията:

б) Тъй като 729 = 3 6 и 1/9 = 3 −2, оригиналният израз може да бъде пренаписан като .

След това прилагаме свойството корен на степен, преминаваме от корен към степен и използваме свойството съотношение на степени, за да преобразуваме основата на логаритъма в степен: .

Като вземем предвид последния резултат, имаме .

отговор:

а) , б) .

Ясно е, че в общия случай, за да се получат степени под знака на логаритъма и в неговата основа, може да са необходими различни трансформации на различни изрази. Нека дадем няколко примера.

Пример.

Какво е значението на израза: а) , б) .

Решение.

Освен това отбелязваме, че даденият израз има формата log A B p , където A=2, B=x+1 и p=4. Числови изразиПреобразувахме този тип според свойството на логаритъма на степента log a b p =p·log a b , следователно с дадения израз искам да направя същото и да премина от log 2 (x+1) 4 към 4·log 2 (x+1) . Сега нека изчислим стойността на оригиналния израз и израза, получен след трансформацията, например, когато x=−2. Имаме log 2 (−2+1) 4 =log 2 1=0 и 4 log 2 (−2+1)=4 log 2 (−1)- безсмислен израз. Това повдига логичния въпрос: „Какво направихме погрешно?“

И причината е следната: извършихме трансформацията log 2 (x+1) 4 =4·log 2 (x+1) , въз основа на формулата log a b p =p·log a b , но имаме право да приложим тази формула само ако са изпълнени условията a >0, a≠1, b>0, p - всяко реално число. Тоест трансформацията, която направихме, се осъществява, ако x+1>0, което е същото като x>−1 (за A и p условията са изпълнени). В нашия случай обаче ODZ на променлива x за оригиналния израз се състои не само от интервала x>−1, но и от интервала x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.

Необходимостта да се вземе предвид DL

Нека продължим да анализираме трансформацията на израза, който сме избрали log 2 (x+1) 4 , а сега нека видим какво се случва с ODZ при преминаване към израза 4 · log 2 (x+1) . В предишния параграф открихме ODZ на оригиналния израз - това е множеството (−∞, −1)∪(−1, +∞) . Сега нека намерим диапазона от приемливи стойности на променливата x за израза 4·log 2 (x+1) . Определя се от условието x+1>0, което съответства на множеството (−1, +∞). Очевидно е, че при преминаване от log 2 (x+1) 4 към 4·log 2 (x+1), обхватът на допустимите стойности се стеснява. И се съгласихме да избягваме трансформации, които водят до стесняване на DL, тъй като това може да доведе до различни негативни последици.

Тук си струва да се отбележи, че е полезно да се контролира ОА на всяка стъпка от трансформацията и да се предотврати неговото стесняване. И ако изведнъж на някакъв етап от трансформацията е имало стесняване на DL, тогава си струва да разгледаме много внимателно дали тази трансформация е допустима и дали сме имали право да я извършим.

За да бъдем честни, нека кажем, че на практика обикновено трябва да работим с изрази, в които ODZ на променливите е такъв, че когато извършваме трансформации, можем да използваме свойствата на логаритмите без ограничения във формата, която вече ни е известна, както от от ляво на дясно и от дясно на ляво. Бързо свиквате с това и започвате да извършвате трансформации механично, без да мислите дали е възможно да ги извършите. И в такива моменти, за късмет, се изплъзват по-сложни примери, в които небрежното прилагане на свойствата на логаритмите води до грешки. Така че трябва винаги да сте нащрек и да се уверите, че няма стесняване на ODZ.

Няма да навреди отделно да се подчертаят основните трансформации, базирани на свойствата на логаритмите, които трябва да се извършват много внимателно, което може да доведе до стесняване на OD и в резултат на това до грешки:

Някои трансформации на изрази, базирани на свойствата на логаритмите, могат да доведат и до обратното - разширяване на ODZ. Например преходът от 4·log 2 (x+1) към log 2 (x+1) 4 разширява ODZ от набора (−1, +∞) до (−∞, −1)∪(−1, +∞). Такива трансформации стават, ако останем в рамките на ODZ за оригиналния израз. Така току-що споменатата трансформация 4·log 2 (x+1)=log 2 (x+1) 4 се извършва в ODZ на променливата x за оригиналния израз 4·log 2 (x+1), т.е. x+1> 0, което е същото като (−1, +∞).

Сега, след като обсъдихме нюансите, на които трябва да обърнете внимание, когато трансформирате изрази с променливи, използвайки свойствата на логаритмите, остава да разберем как правилно да извършваме тези трансформации.

X+2>0. Работи ли в нашия случай? За да отговорим на този въпрос, нека да разгледаме ODZ на променливата x. Определя се от системата от неравенства , което е еквивалентно на условието x+2>0 (ако е необходимо, вижте статията решаване на системи от неравенства). Така можем безопасно да приложим свойството на логаритъм на степента.

Имаме
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =
=3·7·log(x+2)−log(x+2)−5·4·log(x+2)=
=21 log(x+2)−log(x+2)−20 log(x+2)=
=(21−1−20)·log(x+2)=0 .

Можете да действате по различен начин, за щастие ODZ ви позволява да направите това, например така:

отговор:

3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =0.

Но какво да правим, когато условията, съпътстващи свойствата на логаритмите, не са изпълнени в ODZ? Ще разберем това с примери.

Нека трябва да опростим израза log(x+2) 4 − log(x+2) 2 . Преобразуването на този израз, за ​​разлика от израза от предишния пример, не позволява свободно използване на свойството логаритъм на степента. защо ODZ на променлива x в този случай е обединението на два интервала x>−2 и x<−2 . При x>−2 можем лесно да приложим свойството на логаритъм на степен и да действаме както в примера по-горе: log(x+2) 4 −log(x+2) 2 =4 · log(x+2)−2 · log(x+2)=2 · log(x+2). Но ODZ съдържа още един интервал x+2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к log(−|x+2|) 4 −log(−|x+2|) 2и по-нататък поради свойствата на степента k lg|x+2| 4 −lg|x+2| 2. Полученият израз може да се трансформира, като се използва свойството логаритъм на степен, тъй като |x+2|>0 за всяка стойност на променливата. Имаме log|x+2| 4 −lg|x+2| 2 =4·lg|x+2|−2·lg|x+2|=2·lg|x+2|. Сега можете да се освободите от модула, тъй като той си е свършил работата. Тъй като извършваме трансформацията при x+2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .

Нека да разгледаме още един пример, така че работата с модули да стане позната. Нека разберем от израза отидете до сумата и разликата от логаритми на линейни биноми x−1, x−2 и x−3. Първо намираме ODZ:

В интервала (3, +∞) стойностите на изразите x−1, x−2 и x−3 са положителни, така че лесно можем да приложим свойствата на логаритъма на сумата и разликата:

И на интервала (1, 2) стойностите на израза x−1 са положителни, а стойностите на изразите x−2 и x−3 са отрицателни. Следователно на разглеждания интервал представяме x−2 и x−3, използвайки модула като −|x−2|

и −|x−3|

Имаме

съответно. В същото време

Сега можем да приложим свойствата на логаритъма на произведението и частното, тъй като върху разглеждания интервал (1, 2) стойностите на изразите x−1 , |x−2|

• и |x−3|
• - положителен.
• Получените резултати могат да се комбинират:

Подобни резултати са дадени например в инструкциите за решаване на експоненциални и логаритмични уравнения в колекцията от задачи по математика за постъпващите в университети, под редакцията на М. И. Сканави.

Пример.

Опростете израза .

Решение.

Би било добре да се прилагат свойствата на логаритъма на степента, сбора и разликата. Но можем ли да направим това тук? За да отговорим на този въпрос трябва да познаваме ДЗ.

Нека го дефинираме:

Съвсем очевидно е, че изразите x+4, x−2 и (x+4) 13 в диапазона на допустимите стойности на променливата x могат да приемат както положителни, така и отрицателни стойности. Следователно ще трябва да действаме чрез модули.

Свойствата на модула ви позволяват да го пренапишете като , така че

Освен това нищо не ви пречи да използвате свойството на логаритъм от степен и след това да приведете подобни условия:

Друга последователност от трансформации води до същия резултат:

и тъй като на ODZ изразът x−2 може да приема както положителни, така и отрицателни стойности, тогава при поставяне на четен показател 14